三个高中生是如何再一次证明百年数学定理的?
三名高中学生,仅在业余时间,又一次证明了100年前的数学定理。
不只是圆,你可以在那里门格海绵(Menger Sponge)在数学中找到任何一种结(knot)!
你可能不熟悉门格海绵。这是Karl。 Menger(1926年卡尔·门格尔)建立的一个非常有趣的概念,对于现代数学、图形学等领域至关重要。

这款分形海棉在100年间吸引了无数的专业和业余数学家,原因也很简单:它看上去太有趣了。
2014年,100多名数学爱好者还参与了一项名为MegaMenger的全球行动,用名片制作了一种新版本的门格海绵,重约200磅。
由于它具有多孔、泡沫状的结构,也常用于模拟减振器和特殊的空间-时间模式。
它的结构非常优雅。我们应该从一个立方体开始,首先将位于中心和六个面中心的立方体移除。然后对准剩下的。 20 一个正方体重复这个过程。
每一次迭代,它的间隙都会呈指数级增长,最终结构与常见的“海棉”非常相似,这就是它名字的由来。
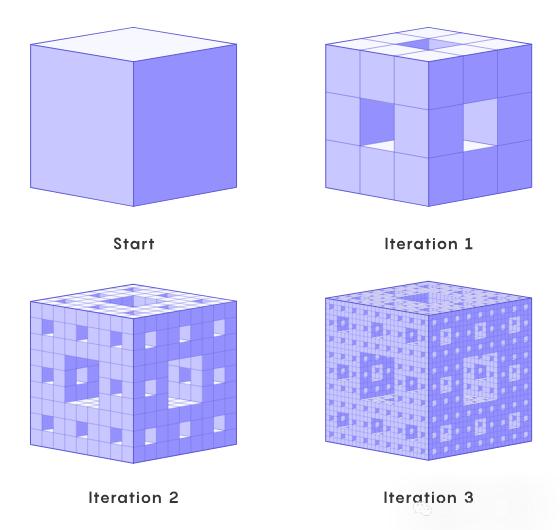
门格海绵还具有很特别的数学特性:在迭代过程中,正方体的形态体积会减小到零,而表面积会无限增大。。
当Menger在1926年提出这个概念时,它证明了这个概念。任何可以想像的曲线——简单的线条和圆形,看起来像树或雪花的结构——可以变形,然后变形。嵌入在海绵的某个地方,换句话说,这种海绵是一种“通用曲线”。
今天的主角来自加拿大的三名高中生,跟随Malors,Malors当时还在读多伦多大学的研究生。 Espinosa(马洛斯·埃斯皮诺萨)进一步扩展了这一定律的证明。
并且他们还发现,三叶结属于类别。 “普雷策尔结(pretzel knot)"也可以映射到门格海绵四面体版本中。
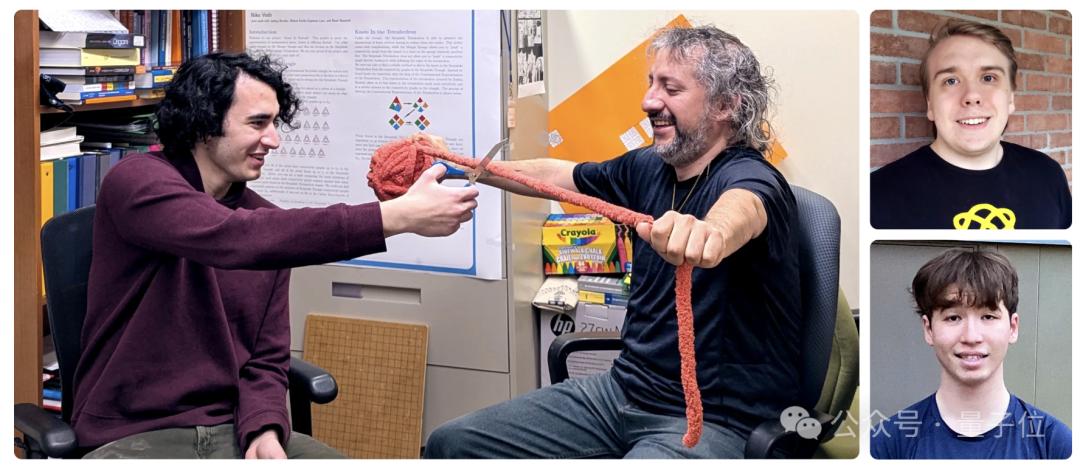
拓扑学家Radmilamila,北卡罗来纳州立大学。 Sazdanovic还评论说,“这是一个非常巧妙的证明方法。”
这个究竟是怎么做到的?
用弧形图和康托尔集表示结结
在阅读了相关证明之后,Malors意识到,Menger已经证明了它可以在他的海绵中找到任何圆圈。
所以,假设是另一种,类似于“圆”形式,这条法律还能成立吗?
例如,一个经典的数学结:扭曲和系结一根绳子,然后封闭两侧形成一个环。这个时候,如果一只蚂蚁沿着它走,它最终会回到原点,就像在圆上一样。
这样,每个结都等同于圆,或者说“同胚”(homeomorphic)”于圆。

从这个想法中,Malors受到了启发,他决定从自己教的高中找一些学生来证明:你可以在门格海绵中找到任何一个结。
之后,三名高中生——Joshua Broden、Noah Nazareth 和 Niko 真的做到了Voth!
三个学生在参加这次证实活动之前,从未做过这样一个“无答案”的问题,但是这群14岁的少年特别兴奋。
它们的目标类似于用一根微针穿过一团灰尘,即海绵经过多次移除后剩下的部分。
她们必须把针插在正确的位置,准确地系好,而且不能离开海棉。假如由于任何一个结,他们的线条都漂浮在海棉的缝隙中,那就失败了。
尽管这个看起来很难,但是有一个简单的方法。在平面上,绳结可以被称为一个特殊的图表。弧表示(arc presentations)。
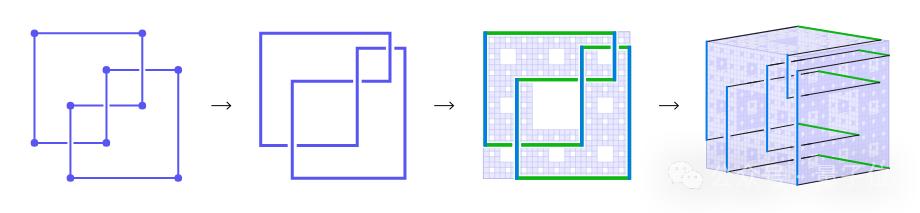
要画出弧形表示图,首先要知道结的股票是如何前后移动的。然后,用一套规则将这些信息转换成网格上的一系列点。网格的每一行和每一列都将包含两个点。
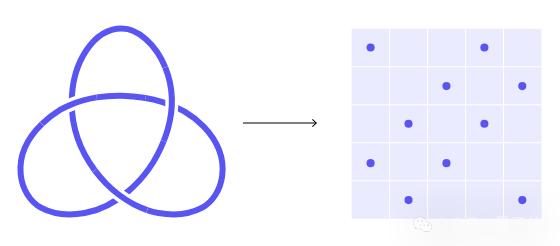
将这些点与水平和垂直线连接起来。每当两个线段交叉时,将垂直线画在水平线上。
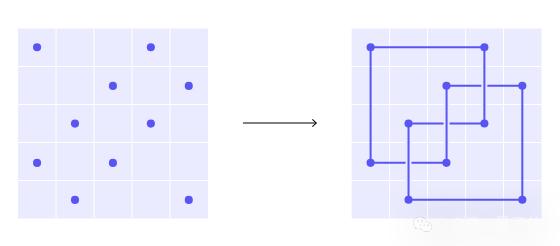
每个结都可以用这个网格来表示。虽然弧形表示有时看起来比其他绘制方法更复杂,但它可以让数学家更容易地研究结的一些重要特征。
在看到纵横交错的线条图时,学生们想到了门格海绵的表面。
您可以很简单地将弧线的水平线放在海棉的一个表面,将垂直线放在海棉的另一个表面。
难点在于如何将结拉申回三维空间。在弧线的每个角落,两个面都需要通过海绵的内部连接起来,以防止遇到洞。
他们想到了这一点,以确保这一点。康托尔集(the Cantor set),门格海绵的一维模拟就是这样。
要构建这个集合,首先要从一个线段开始,分成三部分。去掉中间的三分之一,然后对剩下的两段做同样的处理,等等,无穷无尽。最后剩下的就是零散的点。
研究小组的证明同时使用了门格海绵和康托尔集,它们有相同数量的移除步骤。
他们发现康托尔集中的海绵表面坐标不应该有洞。而且由于海绵的重复设计,这些点后面不应该有洞。因此,结可以随意清晰地穿过海绵,而不是不小心跳出海绵的材料。
接下来,学生能做的就是证明他们可以压缩或申请随机绳结的弧线,使所有角落都与康托尔集中的坐标对齐。(这种压缩和拉申是合理的,因为它不会影响弧线的整体结构,所以也不会影响它所代表的绳结)。
三个学生走了一条捷径,以完成这最后一步。
他们证实,他们可以变形任何弧线,使垂直段和能力段的连接点集中在康托尔。这自动保证了更多的角度将与康托尔集合。
这就是他们在一次迭代中,总能将给定的结嵌入格尔海棉中。。
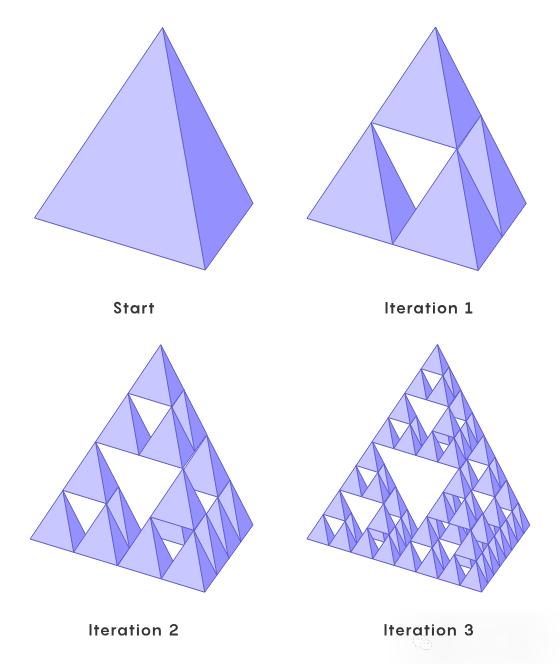
Malors最初的确认已经完成。然而,他们仍然希望进一步推进这项研究:门格海绵四面体版本中是否还可以嵌入所有的结??
Malors最初坚信,对于想要在四面体中找到三叶结的学生来说,这是不可能的。
但是几个星期后,学生们真的做到了:他们找到了一种新的方法,将三叶结的弧表示映射到四面体中。。
后来他们确认,这种方法适用于三叶结所属的更广泛的结类。 “普雷策尔结(pretzel knot)”。
但目前对其它类型结的确认尚未完成。
One More Thing
Malors说,这个证明过程,让学生真正体会到了数学研究的痛苦。
与高中数学题不同,总会给出一个明确的答案,在真正的数学研究中,很大一部分时间都是挣扎在有希望的失败中。
Malors认为学生的证明方法可能是对分形复杂性进行更广泛的测量。提供了一个新的想法。
并不是所有的分形物都能保证所有类型的结的容纳。也许我们可以更好地了解它们的结构,因为它们可以容纳和不能容纳什么类型的结。
最起码,这部作品可以激发新的艺术灵感,类似于2014年的MegaMenger比赛等等。
在确认期间,三名学生都高中毕业了。只有Broden决定在大学学习不忙的时候继续研究四面体问题,但他们都在考虑从事数学工作。
另外一位同学Nazareth也表示:“我正在努力为更多的工作,为真理的本质做出贡献,这是非常有意义的。
参考链接:https://www.quantamagazine.org/teen-mathematicians-tie-knots-through-a-mind-blowing-fractal-20241126/
本文来自微信微信官方账号“量子位”,作者:关注前沿技术,36氪经授权发布。
本文仅代表作者观点,版权归原创者所有,如需转载请在文中注明来源及作者名字。
免责声明:本文系转载编辑文章,仅作分享之用。如分享内容、图片侵犯到您的版权或非授权发布,请及时与我们联系进行审核处理或删除,您可以发送材料至邮箱:service@tojoy.com


