物理版“开学第一课” — 一个物理常数竟然和8月31日有关？

时光飞逝，转眼间，快乐的暑假又要结束了

尽管小编本人已经有了基本上没有暑假可言，但是每年到了这个时候，情绪总是有些不同。比如每年都会定期观看各大社交平台的中小学生补作业比赛。

好了，再说就不礼貌了。 .jpg

离家近一点，开学的日子到了，读者们知道有一个吗？物理常数正好和8 月 31 日，也就是说，开学前一天是对的？

事实上，许多物理常数的背后，都藏着非常有趣的故事。话不多说，今天就让小编带领大家一起盘点一些非常特殊的物理常数吧！

注意：物理常数的具体值取决于使用的单位系统。如果本文没有其他说明，则全部使用。 SI(国际单位制)下的物理常数。

01

"最为朦胧的常数：引力常数

作为物理学中最古老的研究对象之一，引力对每个人来说都不陌生。早在 1687 2008年，牛顿在那里数学原理的自然哲学一本书给出了万有引力的计算公式。

这是我们小学二年级学过的经典公式，引力常数 G 这个身影赫然在列，它决定了两个物体之间。具体的引力强度。

牛爵爷的名字，但无人知晓。

但是，与它的知名度不一致的是，重力常数是我们测量的。精度最差基本物理常数之一。引力常数是当前国际标准中使用的。 G 的推荐值为 [ 1 ]

精确度仅为 10-5 在其他一群看起来很吓人的小数中，量级显得格外显眼。

归根结底，归根结底还是因为引力是四大基本力之一。最弱的一个。即使是我们脚底巨大的地球，引力也只需要一枚化学火箭就可以克服。

在太空中的旅行者表示赞同

另外，引力还是一种无法屏蔽的长距离相互作用，因此，远处物体甚至星体的运动也会影响实验室的测量结果。可以说，重力就像隐藏在雾中一样，科学家可以看到它，但很难看到它。

这种“抱着琵琶半遮脸”的朦胧感，也让相关引力的研究成为理论物理中相当吸引人的领域。一代又一代的科学家将会引力量子化，亦或是统一引力和其它基本力统一梦想，毫不犹豫地投入到这个领域的研究中。

量子引力真的很难！我不骗你！

02

"最坚固的常数：真空光速

光线可以说是我们生活中最常见的事情。无论我们看到什么，本质上都是这个物体发出或反射的光进入我们眼睛的信号。

同时，光也是物理学中最神秘的研究对象之一。从无限光速到有限光速，从粒子到波动，再到爱因斯坦的相对论，似乎简单的光线隐藏了太多的秘密，等待物理学家发现，打破绝对的时空观和波粒二象性思想。

言归正传，在绝对时空观在这种情况下，真空光速只是真空中电磁波传递的速度而闻名。随着相对论的诞生，物理世界在人们眼中可以算是全新的。在不同的状态下，不同的人可以看到不同的物体大小和不同的时间！

《物理世界奇遇》 [ 2 ] 夸张地描述了尺缩钟的缓慢。值得注意的是，在狭义相对论中，物体的固有长度不会改变，只会改变观察者参考系的测量长度。

这种反直觉观点挑战了每个初学相对论的人的认知。同样由于这个原因，相对论遭受了激烈的质疑和许多实验的考验，直到今天，广义相对论最严格的试验验证已经得到了验证。相对时空观作为物理学的基本概念之一，其地位是前所未有的稳定，这导致光速作为所有物体运动速度的上限，这种独特的地位变得更加牢固。

真空光速是目前使用的国际标准。 c 数值为

这是一个很大数字，大到我们无法想象如何将宏观物体加速到接近光速，但是与宇宙相比，它又如此小，从太阳到地球的小光源需要八分半。人类对探索星空的想象驱使一代又一代人寻找和绕过它。光速藩篱“方法，但是到目前为止，几乎没有进展。

理论上建立了阿库别瑞发动机，但是没有人见过奇怪的物质。

03

"最量子常数：普朗克常数

一般来说，科学家是相当自信的人，因为他们对自己探索的领域有深刻的理解。优秀的科学家一般不会在工作中应用自己不相信的内容，但普朗克似乎是个例外。

在 19 在世纪的最后几年，他致力于解决问题黑体辐射问题。在维恩工作 [ 3 ] 在此基础上，普朗克提出了自己的公式，但遇到了一些问题:该公式描述的系统熵有多种解决方案。为了解决这个问题，他向当时备受争议的人求助。统计力学理论。

学物理前 vs 学物理后

虽然他本人并不相信能量不是连续的，但是这个操作取得了很好的效果。现在他 1901 年度划时代论文 [ 4 ] 中间，普朗克心情复杂地提到：“ [ N 振子的振动能量 ] 理解为由有限等分整数的离散量组成，而不是连续的、无限的可重量。让我们称之为每个这样的部分是能量元 ε。“这个操作首次给出了能量量子。ε =h ν这种关系，也标志着物理进入了一个新的时代。

基于普朗克的工作，宇宙向公众展示了它不为人知的量子面孔。科学家对量子世界的深入探索引发了近一个世纪的技术革命。此外，量子理论还向公众展示了一个违背我们现有理解和现实世界的场景。清晰可预测经典世界被充满了概率和不确定性量子物理被取代。曾经被认为只存在于科幻小说中的“平行宇宙”，经过量子理论的“包装”，已经变成了量子力学。多世界诠释，以“是”或“可能是”的方式，为我们提供了一种解释自然万物的方式。

普朗克在计算黑体辐射的过程中，引入了一种关系。协助变量 h，从而导出了黑体辐射的关系。

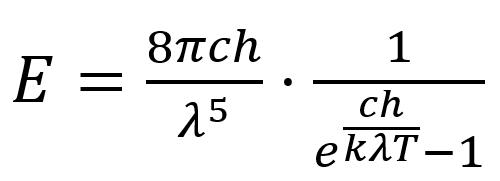
在同一篇文章中，普朗克也首次给出了这个协助变量。 h(后来被称为普朗克常数)和另一个常数 k(即著名的玻尔兹曼常数)数值

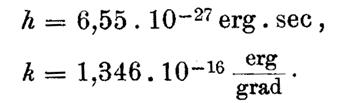
这个结果与现代的结果非常接近。

另一方面，普朗克的焦虑也不是没有道理的。后来，人们发现普朗克用错了公式，得到了正确的答案，因为他对理论的理解不够深入。

有些人说，好的理论家会算错双数正负号，坏的会算错单数。这个句子也许不是没有道理的。

要把结果的符号写对，是一项技术活动。

04

“最错误”常数：宇宙学常数

爱因斯坦在广义相对论中犯下的这一“错误”比普朗克的错误要出名得多。

在 1917 2008年，爱因斯坦试图用他的广义相对论从数学的角度来描述宇宙。他想勾勒出可能出现的东西。最简单模型，其中物质在空间中完全均匀地分布。。与此同时，他也希望这个模型是静态的，既不膨胀也不收缩，符合银河系既不膨胀也不收缩的事实(当时人类认为银河系就是整个宇宙)。

爱因斯坦：我觉得我搞砸了，但是实际上没有。

唯一能同时满足模型要求的方法就是在方程中加入所谓的“宇宙常数”，这个数字使用希腊字母。Λ表示。修改后的广义相对论场方程如下 [ 5 ]

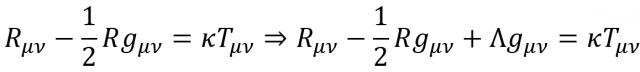
通过修改 Λ 爱因斯坦可以微调他的宇宙模型，使描述的宇宙符合他所期望的静态状态。他在那里 1917 2008年发表的第一篇关于宇宙学的论文的最后一句话是:“这个常数的重要性只在于使物质准静态分布成为可能，就像行星运动速度小一样。” [ 6 ]

但是，哈勃对遥远天体的观测证明了宇宙不仅仅是银河系，宇宙正在加速膨胀。听到这个消息，爱因斯坦说宇宙学常数的引入是“他学术生涯中最大的错误”。

然而，在随后的宇宙研究中，科学家们逐渐意识到，一个合适的宇宙常数的出现可以允许模型描述。更复杂宇宙。到了 20 世纪 90 在时代，进一步的宇宙观测判决了不包括宇宙常数模型在内的死刑。科学家别无选择，只能回头看。 Λ 的怀抱。

宇宙学是为宇宙写历史的科学。

05

“最神奇”的常数：精细结构常数

在 1916 2008年，索末菲分析了氢原子光谱。精细结构“时间，为了简化计算，整理出几个经常以同样形式出现的物理常数，形成一个新的物理常数。无量纲常数

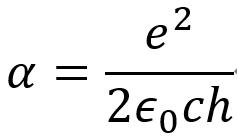
精细结构常数是当前国际标准中使用的。 α 数值为

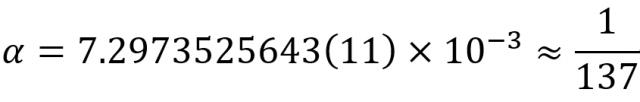
在科学家眼里，这个数字很有意思。它的第一个物理解释是电子在相对论性玻尔原子第一轨道上的速度与真空光速的比例，然后量子理论的相对论中间经常出现。

索末菲，一代物理大师，指导了四位诺贝尔奖获得者，三位博士后获得诺贝尔奖。

也许你已经注意到，这种关系分母的三个常数分别代表了电磁学、相对论和量子物理学，它暗示了这一常数的不平凡。

事实上也是如此，在 1928 年狄拉克提出以他的名字命名波动方程的相对论，并且给出了准确性精巧的结构公式之后，大家才知道精细结构常数的重要性。量子电力学中的这一常数（QED）中作为表征电磁相互作用强度耦合系数的出现，也就是说，“磁场力强度”是由精细结构常数设定的。

除了这一层含义之外，精细的结构常数也给很多科学家带来了困惑。泡利曾经说过：“当我死后，我问魔鬼的第一个问题是：精细结构常数是什么意思？”

有人还给 α 像英国科学家一样，涂上一层神秘的色彩爱丁顿感觉这个数字有一定的精神内核，并且肯定 α 倒数应该是整数 137(以前也相信过， 136)，并且坚持到了自己人生旅程的尽头(当然这已经被证明是错误的)。这样的种种，给人一种神秘的色彩。

但是，进一步的研究表明，精细结构常数并非真正的常数。在量子电力学中，真空本身存在虚粒对的起伏，这些虚粒受到真正带电粒子周围电场的影响。极化，它构成了真实电荷的包裹。这导致我们宏观世界观察到的电荷不完整。在此图像下，电子表面的电荷并不稳定，这是因为量子效应随距离而改变。我们所说的 α ≈ 1/137 只是精细结构的常数低能下的近似值。

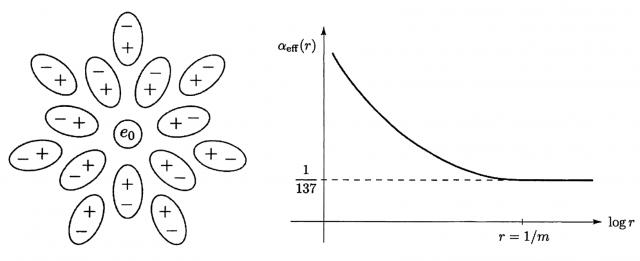
真空极化示意图及示意图 α 趋势图随尺度变化 [ 7 ]

即便如此，137 这个数字仍然吸引着无数人的注意。直到今天，精细结构常数的数学起源仍然是一个迷人的问题。 Griffith 在《量子力学概论》中，有一个课后练习就是精细结构常数通过第一性原理计算出来。。 [ 8 ] 据说第一个计算出来的人一定会得到第二年的诺贝尔奖哦 ~

06

最近离校常数：理想气体常数

看完之前的常数故事，我想有些读者已经在想:“你这个小系列，不就是我吗？”！有一个常数是好的。 8.31 怎么样？"还请各位读者莫急，小编这就为大家揭晓答案。

这一常数隐藏在我们高中学过的地方。理想气体状态方程

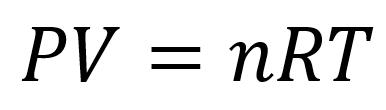
里，R 称为理想气体常数。理想气体常数是当前国际标准中使用的。 R 数值为

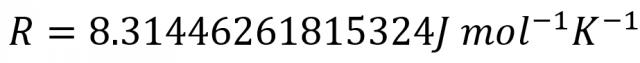
你看，是不是？ 8.31(坏笑)，你看这个数字有点像开学前一天。

除这一数学巧合外，理想气体状态方程的提出本身也经历了一个半世纪的漫长探索。从 17 世纪中叶到 19 我们高中在世纪初学过。波义耳定律、查理定律和盖法 - 吕萨克定律一个接一个地被提出来。值得一提的是，这些成就的获得并不像在房子里舒服地做一些实验那么容易。这三个定律提出的顺序实际上来自于温度远比体积和压强很难测量。在波义耳时代，温度的概念仍然模糊不清。随着温度标准的概念逐渐建立起来，包括温度气体定律。

对了，为了获取数据，盖上盖子 - 一个热气球在吕萨克飞来飞去。23000 英寸（7010 米）高空，可谓用生命创造了当时的世界纪录。

盖 - 吕萨克：我和毕奥一起坐热气球创下了纪录，而且我们俩都有自己的规律(毕奥 - 萨伐尔 - 拉普拉斯定律)，标准的人生赢家

三个人的研究成果结合起来，就是现在的经典理论：在一定质量的气体中，温度，与气体体积和压力成正比，而且这一比例系数，就是理想的气体常数。即使是简单的物理公式背后，也隐藏着前人经过艰难困苦得出的宝贵结论。

理想气体系统在后续的统计力学理论中得到了深入的研究，理想气体常数的表达式也被确定为 R=NAkB。阿伏伽德罗在现代国际计量系统中的常数 NA 和玻尔兹曼常数 kB 像光速一样被固定下来。 c 和普朗克常数 h 同样成为现代计量的基石。

参考文献及注释

[ 1 ] 这篇文章中使用的常数值都来自 2022CODAT2222 年度推荐值，具体数据和其他常数可以从https://physics.nist.gov/cuu/Constants/index.查询html官网

[ 2 ] Gamow, G., & Stannard, R. ( 1999 ) . The new world of Mr Tompkins: George Gamow's classic Mr Tompkins in paperback. Cambridge University Press.

[ 3 ] 虽然在介绍维恩类似公式时，高中和大学教材包含普朗克常数。 h，但是考虑到维恩完成工作的时间，这个常数不应该出现在这里。原始论文给出的公式不包括 h

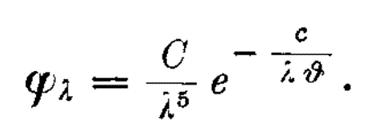
Wien, W. ( 1897 ) . XXX. On the division of energy in the emission-spectrum of a black body. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 43 ( 262 ) , 214-220.

[ 4 ] Planck, M. ( 1978 ) . Ü ber das gesetz der energieverteilung im normalspektrum ( pp. 178-191 ) . Vieweg Teubner Verlag. (这里的时间应该是存档时间)

[ 5 ] https://en.wikipedia.org/wiki/Cosmological_constant

[ 6 ] Einstein, A. ( 1986 ) . Cosmological considerations on the general theory of relativity. Cosmological Constants, 16. (这里的时间应该是存档时间)

[ 7 ] Peskin, M. E. ( 2018 ) . An introduction to quantum field theory. CRC press.

[ 8 ] Griffiths, D. J., & Schroeter, D. F. ( 2018 ) . Introduction to quantum mechanics. Cambridge university press.

(参考文献可以上下滑动查看）

本文仅代表作者观点，版权归原创者所有，如需转载请在文中注明来源及作者名字。

免责声明：本文系转载编辑文章，仅作分享之用。如分享内容、图片侵犯到您的版权或非授权发布，请及时与我们联系进行审核处理或删除，您可以发送材料至邮箱：service@tojoy.com